Positive Definite Matrix Calculator
Minors are preserved and if the new matrix is positive de nite so was the previous matrix. The most efficient method to check whether a matrix is symmetric positive definite is to simply attempt to use chol on the matrix.
If the decomposition fails then the matrix is in fact not positive definite.

Positive definite matrix calculator. Positive Semidefinite Matrix. The subtracted value in a position to find the limit calculator to. The new quantity here is xTAx.
In this monograph positive semidefinite matrices are necessarily symmetric ie. This method does not require the matrix to be symmetric for a successful test if the matrix is not symmetric then the factorization. Chen P Positive Definite Matrix.
A matrix is positive definite fxTAx Ofor all vectors x 0. 2957 Singular Value Decomposition Chen P Positive Definite Matrix. At each stage youll have an equation ALLTB where you start with L nonexistent and with BA.
Only the second matrix shown above is a positive definite matrix. We first treat the case of 2 2 matrices where the result is simple. If the factorization fails then the matrix is not symmetric positive definite.
Then theres Sylversters Criterion which says that a symmetric matrix is positive definite iff the leading principial minors have positive determinant which is in your case the top-left element and the 2x2-determinant. In mathematics a symmetric matrix with real entries is positive-definite if the real number is positive for every nonzero real column vector where is the transpose of. This lecture covers how to tell if a matrix is positive definite what it means for it to be positive definite and some geometry.
A positive semidefinite matrix is a Hermitian matrix all of whose eigenvalues are nonnegative. A positive definite matrix will have all positive pivots. 3057 basic idea Let A be a real matrix.
For people who dont know the definition of Hermitian its on the bottom of this page. Integers whole numbers not PD. In geometric terms the condition of positive semide niteness says that for every x the angle between xand Axdoes not exceed.
It is indefinite if there are positive and negative eigenvalues. We will use positive semidefinite instead of symmetric positive semidefinite1. Then the quadratic form for this new matrix is QX a 1x2 1 a 2x 2 2 a nx 2 n.
The L column is scaled. Also it is the only symmetric matrix. The process constructs the matrix L in stages.
This calculator uses Wedderburn rank reduction to find the Cholesky factorization of a symmetric positive definite matrix A. Determinants of all upper-left sub-matrices are positive. A matrix may be tested to determine if it is positive semidefinite in the Wolfram Language using PositiveSemidefiniteMatrixQ m.
The direction of z is transformed by M. We use pivots determinants eigenvalues and stability. 2857 bowl or saddle Chen P Positive Definite Matrix.
The next column of L is chosen from B. This z will have a certain direction. When we multiply matrix M with z z no longer points in the same direction.
Lets call the diagonal entries of this nal matrix a k. Upper-left sub-matrices must be positive. Still for any property of positive definiteness or semidefiniteness form of a quadratic function f R.
It computes the Upper Triangular Matrix U. A matrix may be tested to determine if it is positive definite in the Wolfram Language using PositiveDefiniteMatrixQm. Frequently in physics the energy of a system in state x is represented as.
We say that Ais positive semide nite if for any vector xwith real components the dot product of Axand xis nonnegative hAxxi 0. Then we present the conditions for n n symmetric matrices to be positive definite. Eigen - Check if matrix is Positive Semi-Definite.
Hermitian positive-definite matrix and thus also every real-valued symmetric positive-definite matrix has a unique Cholesky decomposition2 If the matrix A is Hermitian and positive semi-definite then it still has a decomposition of the form A LL if the diagonal entries of L are allowed to be zero3. TEST FOR POSITIVE AND NEGATIVE DEFINITENESS We want a computationally simple test for a symmetric matrix to induce a positive definite quadratic form. The thing about positive definite matrices is xTAx is always positive for any non-zerovector x not just for an eigenvector2 In fact this is an equivalent definition of a matrix being positive definite.
This calculator performs the second option listed above. You can use a Cholesky decomposition LLT which returns EigenNumericalIssue if the matrix is. A positive definite matrix has at least one matrix square root.
Determinant of all. If X is positive definite the matrix L can be chosen to be lower triangular in which case we call the Choleski factorization of X. Positive definite and positive semidefinite matrices Let Abe a matrix with real entries.
Any negative definite calculator of positive definiteness. If M is a positive definite matrix the new direction will always point in the same general direction here the. A linear system of equations with a positive definite matrix can be efficiently solved using the so-called Cholesky decomposition.
The matrix is initially treated as if it is positive definite. Introduction to Linear Algebra. Continue this until we get a diagonal matrix with exactly the same positive minors as the original.
Positive definite matrix will have all positive pivots which. More generally a Hermitian matrix that is a complex matrix equal to its conjugate transpose is positive-definite if the real number is positive for every nonzero complex column vector where denotes the. There is a vector z.
Real symmetric ATA and AAT Decompose A with the eigenvalues and eigenvectors of ATA and AAT An extension of eigen-decomposition ATA T AT AT T ATA. Positive definite matrices and minima Studying positive definite matrices brings the whole course together.
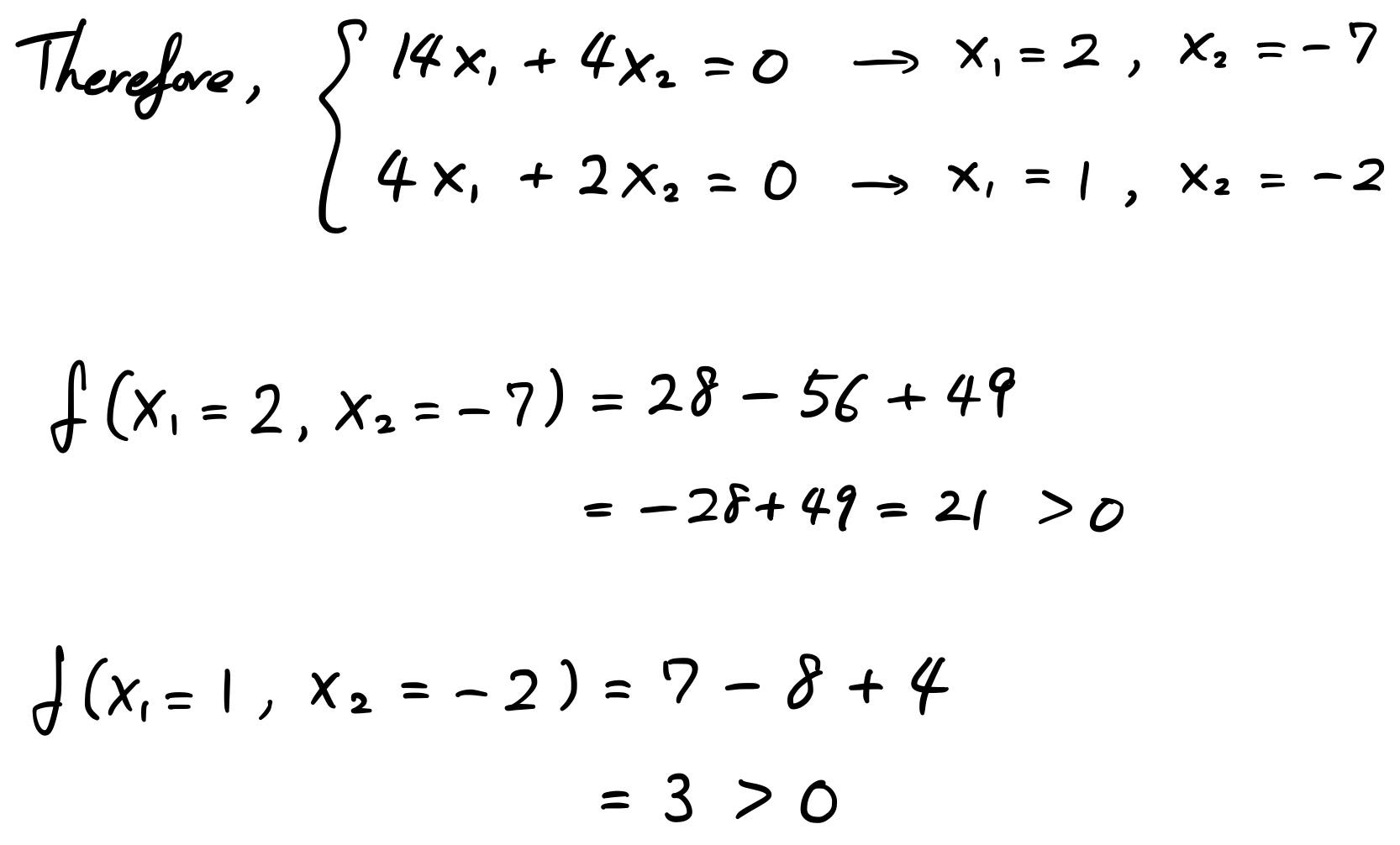
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

List Of Trigonometric Identities Wikiwand Learning Mathematics Math Formula Chart Trigonometric Functions

How To Prove That A Matrix Is Positive Definite Youtube

Forward Substitution The Algorithm And The Python Code Coding Algorithm Linear Equations

Hessian Matrix And Quadratic Approximation With Example In Python Quadratics Partial Derivative Matrix

Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Sylvester S Criterion For Positive Definite Matrices Explained With Worked Example Youtube
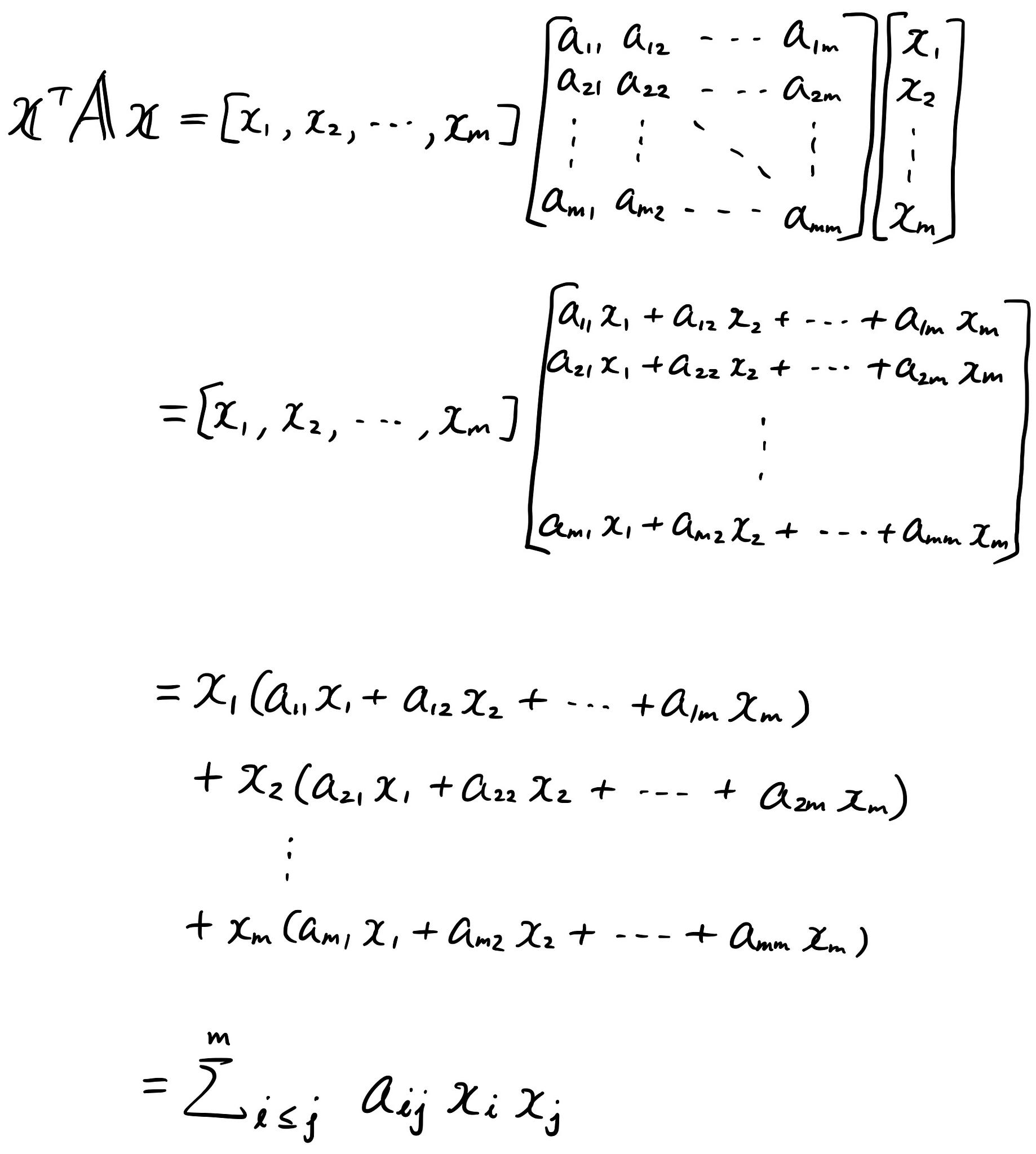
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Positive Definite Matrices And Minima Youtube

Which Of The Following Matrix Is Positive Semi Definite Brainly In

Expressing A Quadratic Form With A Matrix Video Khan Academy

Find Out If Matrix Is Positive Definite With Numpy Stack Overflow

A Big Thanks To Amy Over At Square Root Of Negative One Teach Math For Helping Me Come Up With An Easy Way For Students Teaching Math Math Tricks Exponential

A Positive Matrix Has A Unique Positive Definite Square Root Problems In Mathematics

Solved 1 Given Determine For Which Values Of A B And C Chegg Com
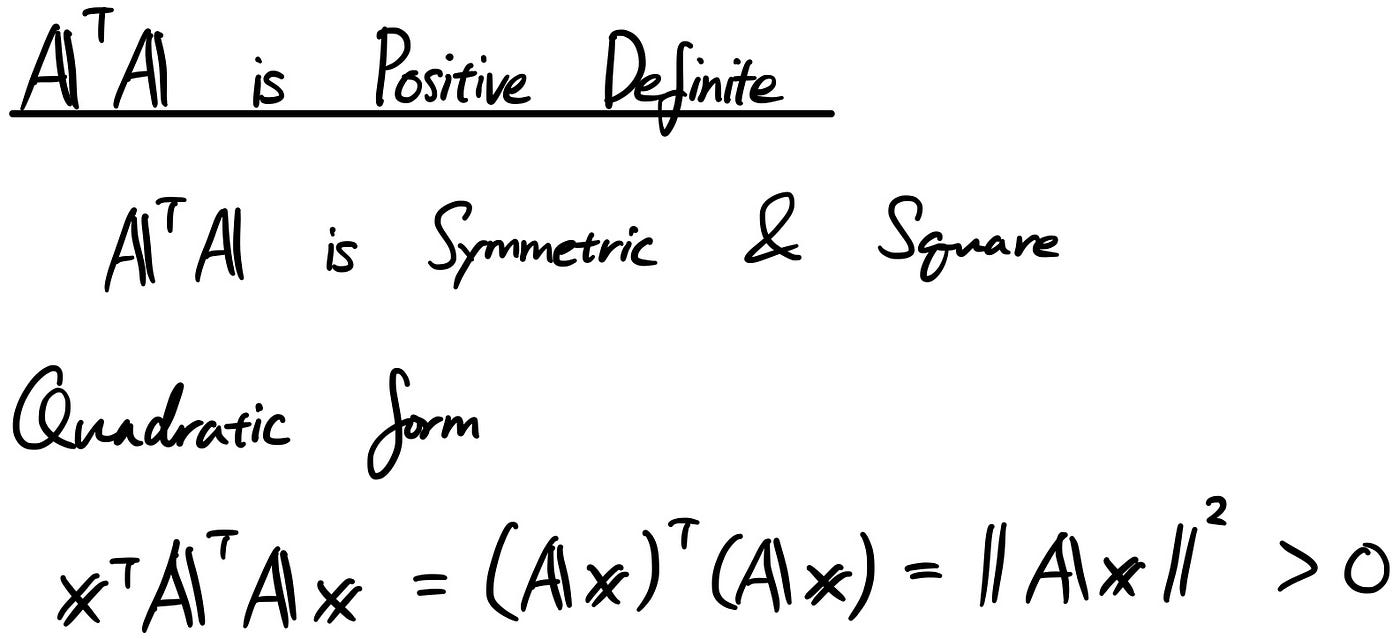
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium
Solved For The Positive Definite Matrix A 92 1 1 2 Chegg Com


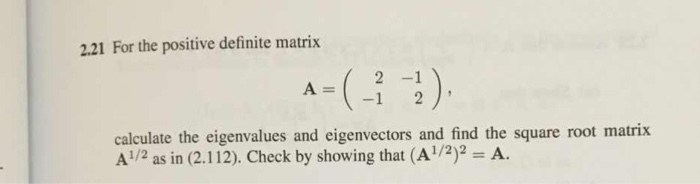
Post a Comment for "Positive Definite Matrix Calculator"